Lid-driven cavity case with Fluent2D and KratosStructure2D
This case is an FSI-adaptation of the famous lid-driven cavity case, calculated using Fluent and KratosMultiphysics StructuralMechanicsApplication. Here, the bottom wall is deformable and an oscillatory velocity is applied at the top.
The oscillatory x-component of the velocity is applied not only at the top, but also in a region at the upper left side wall. As shown in the figure above, the velocity increases linearly with the height. The y-component of the velocity is zero. The oscillating velocity \bar{v} is given by $$ \bar{v}=1-\cos\left(\frac{2\pi t}{5}\right), $$ with t the time. On the corresponding region on the right side, zero pressure is applied. The deformable bottom is fixed at the corners.
The fluid parameters are:
- density: 1 kg/m³
- dynamic viscosity: 0.01 Pa\cdots
The deformable bottom is fixed at its left and right side and consists of a linear elastic material with the follwing properties:
- density: 500 kg/m³
- modulus of elasticity: 250 Pa
- poisson's ratio: 0.0
The total simulated time is 70 s in time steps of 0.1 s.
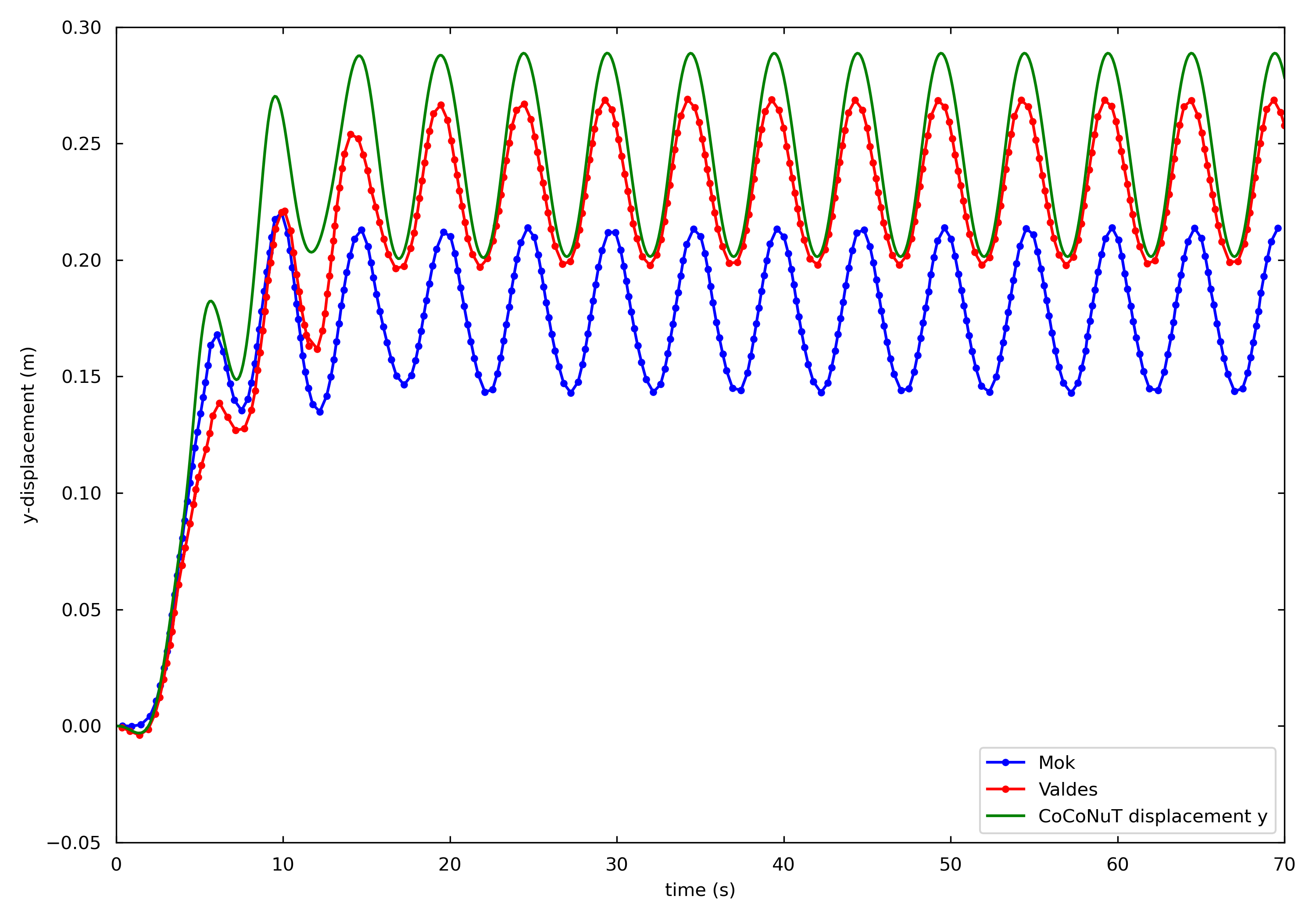
Reference solutions are available from Mok [1] and Valdes [2]. The figure belows shows a comparison with the solution of the examples with Fluent and OpenFOAM.
The following figures show contour plots of the pressure and velocity for this example (with Fluent).
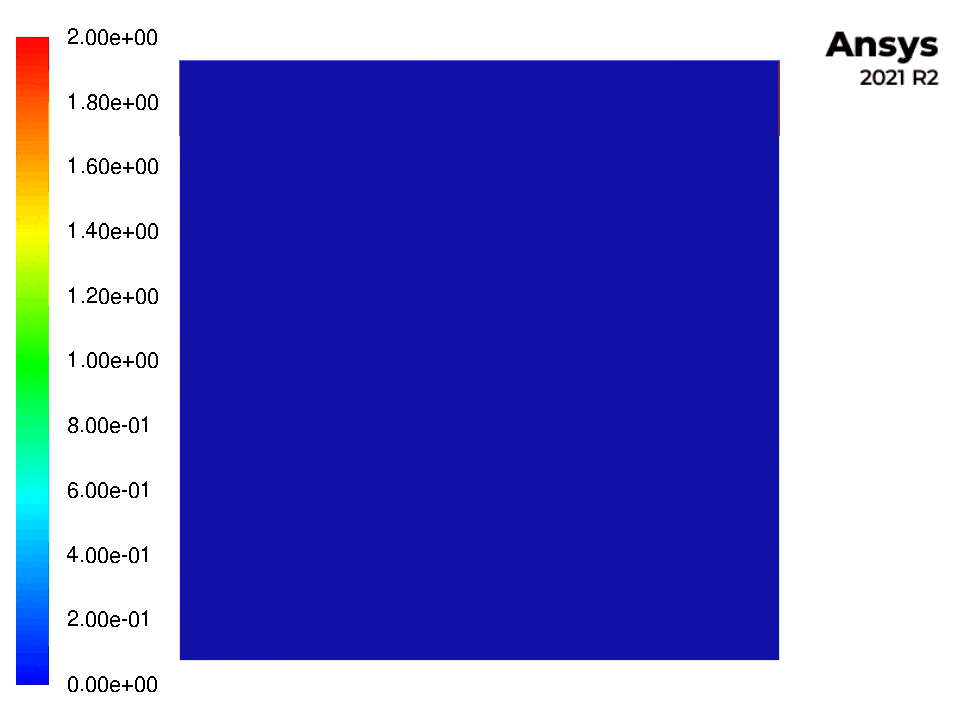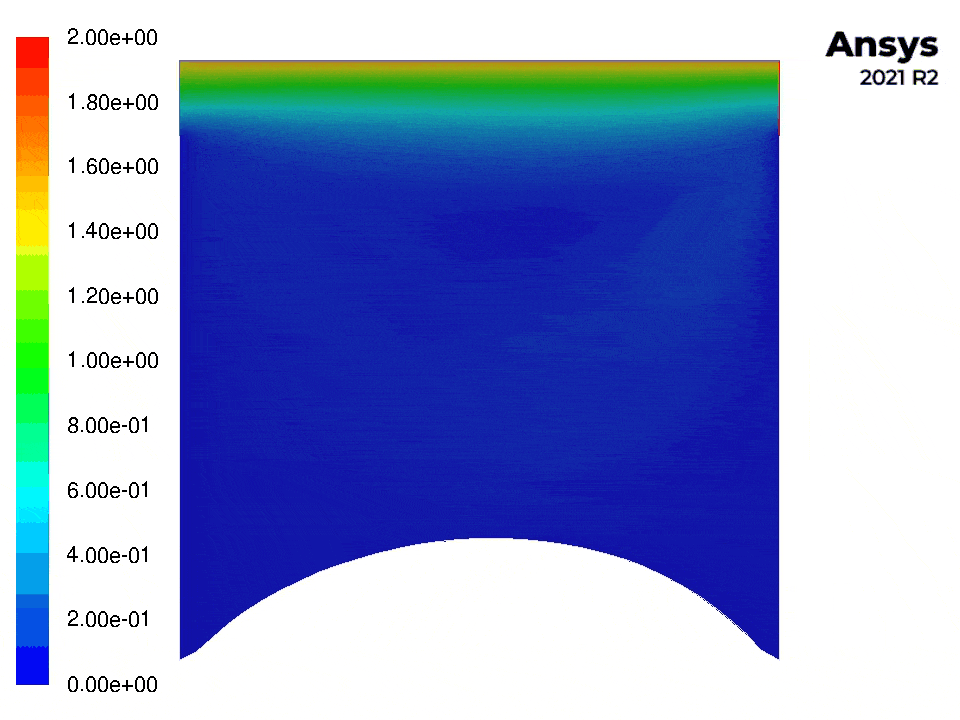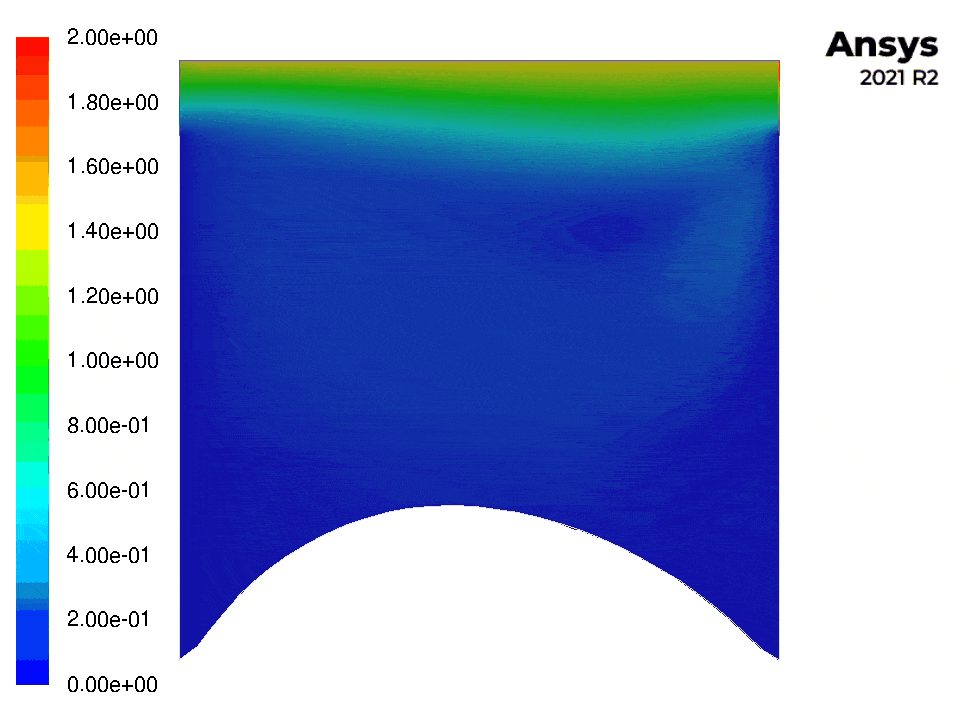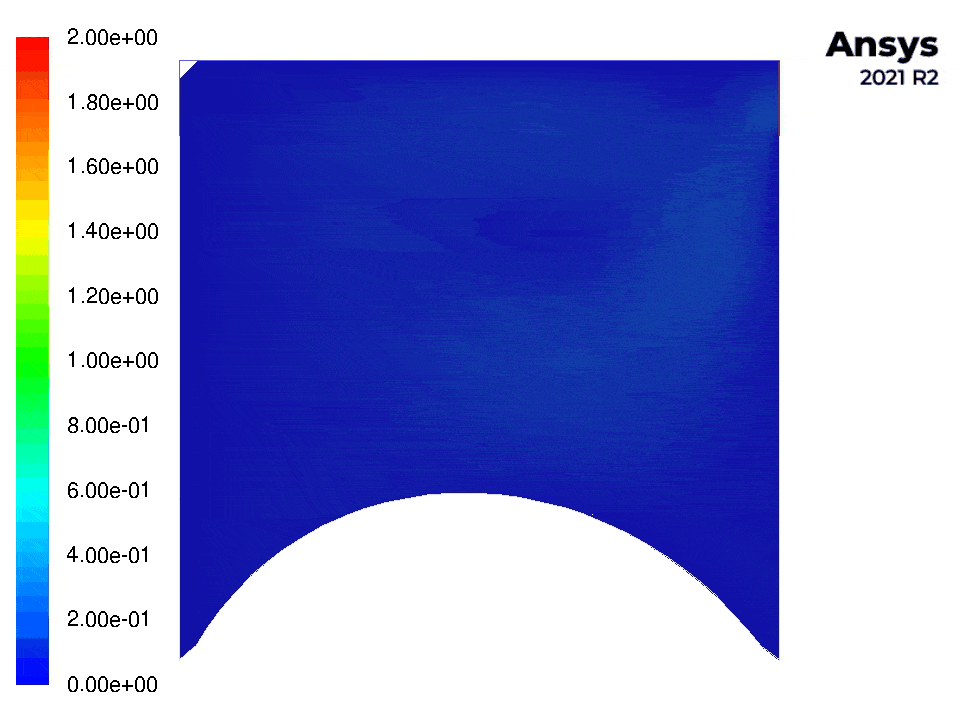
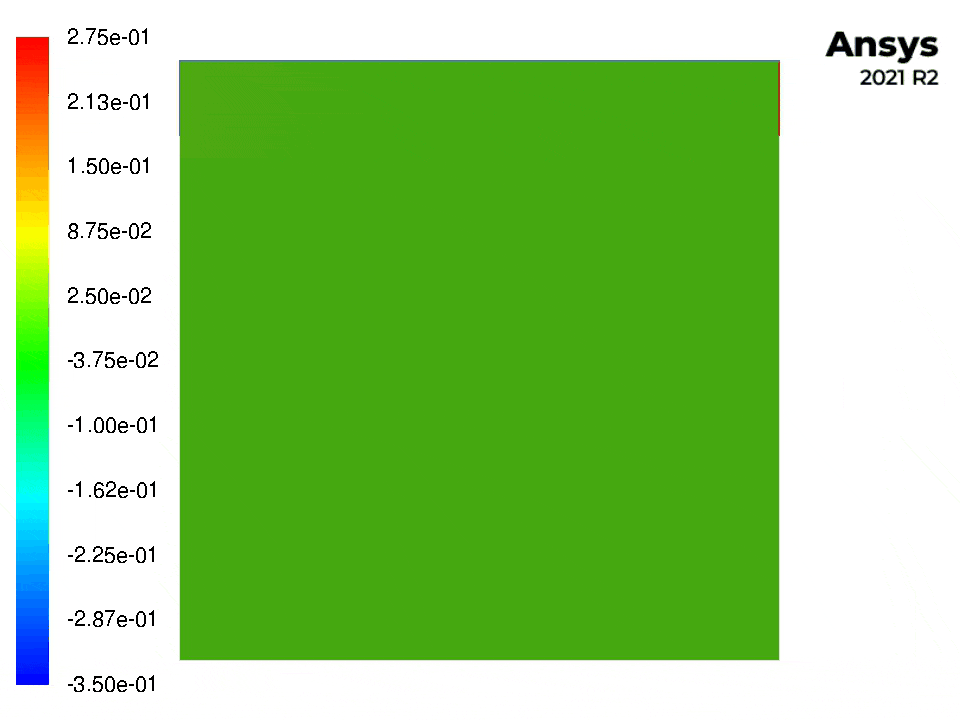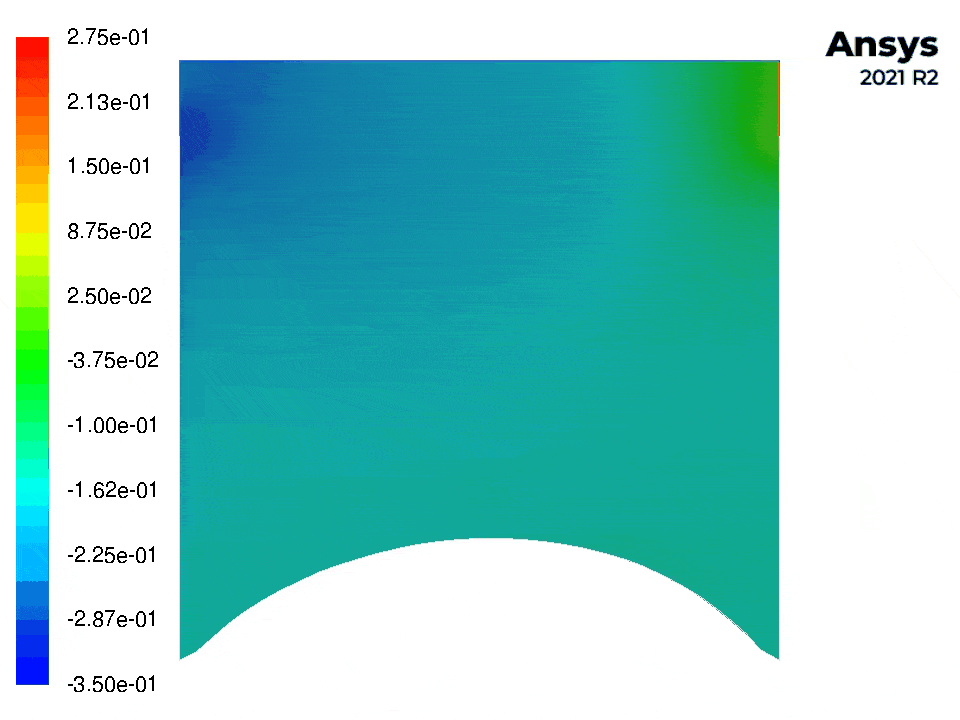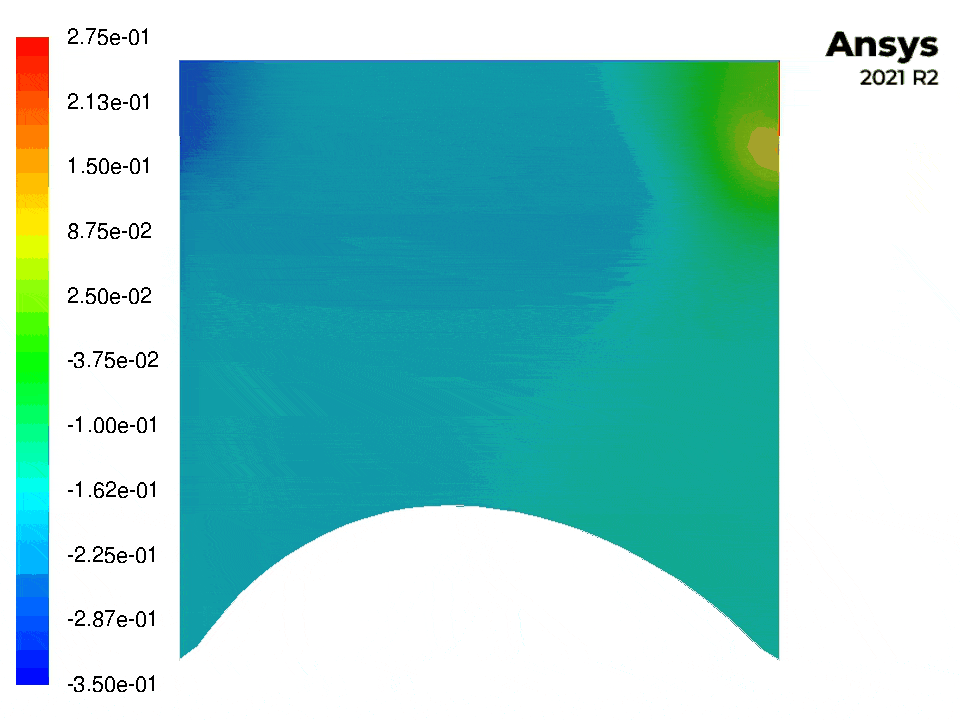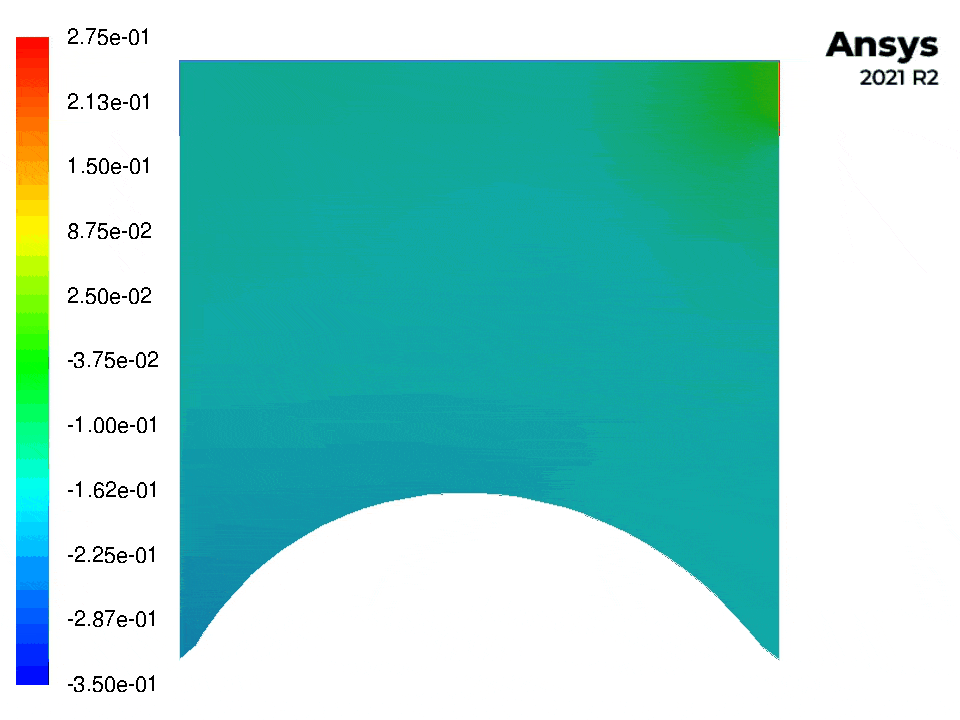
A script evaluate_benchmark.py is provided to compare the results with the benchmark results in [1] and lid_driven_cavity_.
Furthermore, the script animate_lid_driven_cavity.py can be used to visualize the interface data throughout the calculation.
Coupling algorithm
The coupling technique used is the interface quasi-Newton algorithm with an approximation for the inverse of the Jacobian from a least-squares model (IQN-ILS).
No reuse is employed, so the reuse parameter q is set to 0.
Predictor
The initial guess in every time step is done using the linear predictor.
Convergence criterion
Two convergence criteria have been specified:
- The number of iterations in every time step is larger than 15.
- The residual norm of the displacement is smaller than 10^{-9}.
When either criterion is satisfied the simulation stops.
Solvers
Fluent is used as flow solver. A quadrilateral mesh is used with 32 cells on each side of the cavity. A script to regenerate it using Gambit is included. This script allows to change the resolution and geometrical parameters. Dynamic mesh motion is achieved using a spring method.
The structural solver is KratosMultiphysics StructuralMechanicsApplication (abbreviated KratosStructure). The deformable bottom is meshed with 2 layers of 32 TotalLagrangianElement2D4N elements. The movement of the left and right side is constrained.
To exchange information between the solvers on the fluid-structure interface, the use of mappers is required. In the structural solver wrapper, a linear interpolation mapper is used to interpolate in the x-direction from and to the coupled solver.
References
[1] Mok D. P., “Partitionierte Lösungsansätze in der Strukturdynamik und der Fluid−Struktur−Interaktion”, PhD thesis: Institut für Baustatik, Universität Stuttgart, 2001.
[2] Valdés G. and Gerardo J., “Nonlinear Analysis of Orthotropic Membrane and Shell Structures Including Fluid-Structure Interaction”, PhD thesis: Universitat Politècnica de Catalunya, 2007.